Επειδή είδα κάποια post regarding assembly και C++ (και κυρίως MMX,SSE,SSE2 etc) είπα να κάνω και γω ένα post που μπορεί να βοηθήσει κάποιους η ακόμα δώσει εναύσματα σε κάποιους για περαιτέρω διάβασμα! Βασικά αυτό είναι ένα άρθρο παρα post... οποιος έχει όρεξη να κάτσει να ασχοληθεί παραπάνω ας μου πει...γιατί πάνω σε τέτοια έχω κάψει πολλά βραδια! Για να το διαβάσει κανεις αυτό το άρθρο θα πρέπει να έχει στοιχειώδης γνώσεις assembly και C++, δεν θα μπω σε λεπτομέρειες ούτε να γίνω πολύ περιεκτικός πάνω σε αυτό διότι είναι πολύ εξειδικευμένο θέμα από την μάνα του και θα είναι δυσανάγνωστο! Επίσης έχω ένα πρόβλημα στο να γράφω ελληνικά και χρησιμοποιώ με copy paste το πολύ χρήσιμο εργαλείο που μου έδωσε ο KelMan (τον ευχαριστώ πολύ) και ότι βλέπετε είναι σε greeklish και copy paste από αυτό :P.
Βασικά επειδή και πολύ ακόμα αρέσκονται στο game development θα δείξω ένα πολύ interesting topic (κατ εμέ ofc) πως θα φτιάξουμε ένα αλγόριθμο ο οποιος θα κάνει πολύ γρήγορα Vector Normalization. Να υπενθυμίσω πως Vector είναι στα ελληνικά το διάνυσμα, όπου ο μαθηματικός ορισμός του διανύσματος είναι ένα μέγεθος το οποιο έχει φορα, κατεύθυνση και μέτρο. Όπως πριν αρχίσουμε πρέπει να ξέρουμε πως ο υπολογιστής αποθηκεύει τους Vector, τον αποθηκεύει με την Μορφή πινάκων και συγκεκριμένα με την μορφή:
// Sample Vector Struct
// Where sampleVec.index[0] [ x coordinate compoment of Vector ]
// sampleVec.index[1] [ y coordinate compoment of Vector ]
// sampleVec.index[2] [ z coordinate compoment of Vector ]
// sampleVec.index[3] [ d coordinate compoment of Vector ]
// Note d is a dummy var and should be set always to 1, this is an essential step to define it
// as it's required for the matrix math to work! :O
struct sampleVec {
float index[3];
};
struct sampleVecObsolete {
int index[2];
};
Τώρα λίγα λόγια για την assembly. Όπως έχει βγάλει η ISO το standard για τις C++ για την assembly (ISO-14882) μας δίνη native την επιλογή να χρησιμοποιήσουμε Native asm code μέσα στα C++ φιλε μας. Αυτό ήταν ένα πολύ βασικό πλεονέκτημα έναντι άλλων γλωσσών μιας και δίνη την δυνατότητα να παράγεις παρα πολύ γρήγορο κώδικα μιας και η assembly είναι (αν όχι) η γρηγορότερη γλώσσα προγραμματισμού, με το κόστος φυσικά του χρόνου καθώς ο προγραμματισμός σε assembly απαιτεί γνώσεις πάθος και μαζοχισμό...Όπως ένα υπάρχει ένα κακό αυτό το στάνταρ δεν κάνει ακριβές define το πως πρέπει να έχει γίνει το implementation των asm εντολών σε κάθε compiler (για περισσότερες λεπτομέρειες αναζητήστε κάτι που λέγεται manual :P) όμως επειδή πιστεύω πως οι περισσότεροι χρησιμοποιείτε MS Compiler θα δώσω ένα link του msdn στο τέλος για περισσότερες πληροφορίες! Όμως η Microsoft όπως πάντα έχει το δικό της δρόμο και δεν ακόλουθη στο ISO-asm sdr και χρησιμοποιεί αντί για asm έναν δικό της keyword το __asm! Ένα παράδειγμα είναι πχ:
void main( /* main func args */ )
{
// Application Entry code
// ....
// asm code
__asm { ;Assembly code is placed here }
// More Application Code
// blah blah!
return; // End
}
Επίσης παρατηρήστε πως μέσα στα __asm { } brakets δεν ακολουθούνται πια οι κανόνες τις C/C++ παρα μονο τις assembly Note πως το ";" δεν χρειάζεται για να τελειώσεις μια γραμμή αλλα για να κανεις Notes! Τελοσπάντων enough said, ας πιάσουμε δουλειά!
Είμαι σίγουρος πως όσοι δεν γνωρίζετε assembly θα αναρωτιέστε πως λειτουργεί ο assember. Well για να πω την αλήθεια τα πιο σημαντικά κομμάτια του assembler είναι οι Registers, imagine em σαν πολύ μικρά κομμάτια μνήμης που βρίσκονται στον επεξεργαστή όπου μπορούν να αποθηκευτούν δεδομένα. Όμως αυτό τι διαφορα έχει από τις κοινές μας μεταβλητές, που ουσιαστικά και αυτές ικανοποιούν τον ίδιο σκοπό? Η διαφορα ιάνει πως η μια (variable) έχει types δηλαδή int, int64, float etc ενώ η άλλη (συνήθως) δεν έχει types είναι just 0 η 1 :p. επειδή δεν θέλω να το κάνω πολύπλοκο θα παίξουμε με του γενικού τύπου Registers (dunno εάν το μετέφρασα κανονικά είναι General Purpose Registers κανονικά, arg αυτά τα Greek!), αυτές είναι στην περίπτωση μας EAX, EBX, ECX και EDX. Κάθε μια από αυτές είναι 32 bits και χωράει να κάνουμε store μια 32bit int μεταβλητή (όχι int64 etc) εάν θέλετε πάλι δείτε ποσο χώρο στον compiler θέλει ο κάθε type τις C/C++ χρησιμοποιήστε την sizeof() για να δείτε ακριβώς τα bits που χρειάζονται. Ok τώρα ας παίξουμε λίγο με τις Registers! ^_^
int sampleFunction( /* fun args */ )
{
// Normal Variable
unsgined int i = 0;
// Enter assembly mode :)
__asm {
mov eax, i ; This line moves i variable to eax register
add eax, 12 ; This line adds 12 to the eax register, meaning that now eax equals eax+12 or i+12
mov eax, i ; This line moves back eax register to i variable
; 3 Lines to make a simple Addition Operation... heh, pretty much
}
// Exit assembly mode
// Now our i variable equals to 12 since it was initialy 0, let's return it
return i;
Aμα την τρέξετε αυτή την function θα δείτε πως το αποτέλεσμα θα είναι 12. ΠΡΟΣΟΧΉ! Ο assembler έχει δικό του notation και καλο θα ήταν εάν θέλετε να μια πλήρη γεύση για το τι παίζει καλύτερα να κάνετε κάποια μικροπαραδείγματα just to get the feel of it! θα δώσω άλλο ένα παράδειγμα με τις χρήσεις των registers για να δείτε:
int sampleFunction( /* fun args */ )
{
// Normal Variable
unsigned int i = 5;
// Enter assembly mode :)
__asm {
mov eax, i ; This line moves i variable to eax register
_LABEL1: ; This is a jump Label
dec eax ; This line Decriments eax by 1
jz _PROCCED ; If the result of the previous operation was Zero jump to _PROCCED label else procced to the next line
jmp _LABEL1 ; This line forces the program to Jump to _LABEL1
_PROCCED ; This is a jump Label
xor eax, 0xFFFFFFFF ; Notice the Hex number here!
mov eax, i ; This line moves back eax register to i variable
}
// Exit assembly mode
// Now our i variable equals to the max number that a 32 bit can store, let's return it
return i;
Το τι κάνει το πρόγραμμα το αφήνω να το κάνετε compile και να το δείτε μονοι σας...;). Επίσης εάν θέλετε να πειραματιστείτε βάλτε και αλλα intructions ανάμεσα στα labels και δείτε πως αντιδράει το πρόγραμμα επίσης δοκιμάστε να αλλάξετε τον τύπο της μεταβλητής "i" από unsigned σε signed ;)
Τώρα θα πάμε σε κάτι όχι και τόσο βασικό (για αρχαριους) που λέγεται SIMD. Επειδή δεν θέλω να αραδιάσω 6-7 σελίδες με geek technical stuff, για αυτό θα σας δείξω με λίγα λόγια τι κάνει. Όταν θες να κανεις manipulate κάτι είτε αυτό είναι σε assembly είτε σε C++ είσαι υποχρεωμένος να κανεις ένα πράγμα την φορα για παράδειγμα εάν θέλουμε να προσθέσουμε στο j και στο η +1 θα πρέπει:
int j,i = 0;
j = 10;
i = 12;
// One instruction for i
i++;
// One instruction for j
j++;
Aρα για να το κάνουμε αυτό θέλουμε 2 εντολές και ας πραγματοποιούμε την ίδια διαδικασία (δηλαδή increment) και στις 2 εντολές που δώσαμε, Αυτό το technique λέγεται και αλλιώς SISD (Single-Instruction-Single-Data), δηλαδή ότι βασικά ο CPU μπορεί να κάνει calculate ένα value at a time, ενώ εάν θες να κανεις calculate 2 values θα πρέπει να δώσεις 2 statements καταναλώνοντας έτσι διπλό χρόνο από ότι ένα μονο calculation.
Τώρα ας μπούμε στο θέμα, imagine the world of 3D graphics full apo Matrices, Vectors και όλα να είναι multidimentinal data τα οποια πρέπει να επεξεργαστούν όσο πιο γρήγορα γίνετε!! Εάν ήθελες να προσθέσεις 2 Vectors με SISD θα εγγραφες κάτι σαν και αυτό:
// imagive 2 instances of sampleVecObsolete struct named as Vec1, Vec2;Now to add them we would use
// x
Vec1.x = Vec1.x + Vec2.x;
// y
Vec1.y = Vec1.y + Vec2.y;
// z
Vec1.z = Vec1.z + Vec2.z;
// d is a dummy value required for matrix operation (multiplication) and not here ( it's declared in the other Struct)
// Never add the last value of any matrix in 3D Graphics...it's a tip... to avoid dissasters
Αλλα φανταστείτε τώρα να υπήρχε η δυνατότητα από την CPU να πραγματοποιήσουμε και τα 3 instructions μαζί δηλαδή να προσθέσουμε και τα 3 compoments των 2 vectors μαζί χωρίς περαιτέρω κόπο, in fact that's what's SISD is all about! Πιστεύετε το η όχι το SISD υποστηρίζεται από τα περισσότερα CPU τις αγοράς. Από την εισαγωγή των εντολών MMX τις Intel που ήταν μονο για Integer values (μεγάλο breakthough για την εποχή) ήρθε και η ώρα να λανσαριστούν και οι εντολές SSE που SSE είναι short για Streaming SISD Extentions και έδωσε την δυνατότητα για να κάνουμε πολύ fast multimedia programming για πρώτη φορα! Διότι έφερε το SISD σε float variables. Με την πρώτη εκδώσει των ΣΕ μπορείς να εκτέλεσις 4 32bit floats το οποιο είναι extremely useful όταν εξής να κανεις με 3D Programing ( 3D Vectors [x,y,z,d], 3D Matrices [2x2,3x3 or 4x4 array], High Color Graphics [ R,G,B,A] etc ). Ωραία τα λόγια αλλα πως μπορούμε να το χρησιμοποιήσουμε στις εφαρμογές μας? Πολύ απλά, σήμερα σχεδόν όλοι οι CPU έχουνε τις SSE αλλα όχι όλοι για να είμαστε σίγουροι θα πρέπει να τσεκάρουμε το CPUid το οποιο υπάρχει σε κάθε Intel compatible CPU. Στις εφαρμογές σας θα πρέπει να έχετε 2 implementation ένα που θα το χρησιμοποιεί εάν είναι διαθέσιμες οι εντολές SSE και μια όταν δεν είναι, έτσι θα είστε ασφαλισμένοι 100 %. Ένα τέτοιο πρόγραμμα το οποιο ελέγξει εάν είναι supported θα έμοιαζε κάπως έτσι:
void main( /* function args */)
{
// Set up our Values
unsigned int cpeinfo;
unsigned int cpsse3;
// Enter asm mode
__asm
{
mov eax, 01h ;01h is the parameter for the CPUID command below
cpuid ; We took the CPUid, now let's store the info where we want
mov cpeinfo, edx ;Get the info stored by CPUID
mov cpsse3, ecx ;info about SSE3 is stored in ECX
}
// End asm mode
// Now let's out put our results
cout << "1 - Instruction set is supported by CPU\n";
cout << "0 - Instruction set not supported\n";
cout << "--------------------------------\n";
// Here we check for the support !!
cout << "MMX: " << ((cpeinfo >> 23) & 0x1 ) << "\tSSE: " << ((cpeinfo >> 25) & 0x1 ) << "\tSSE2: " << ((cpeinfo >> 26) & 0x1 ) << "\n";
cout << "SSE3: " << ((cpsse3 ) & 0x1 );
}
Τώρα για να δούμε εάν ο compiler μας σίγουρα μπορεί να καταλάβει ΣΕ προσπαθήστε να κάνετε compile το παρακάτω:
struct sampleVecObsolete {
int index[2];
};
void main( /* func args */ )
{
// Make a Vector Instance
samleVecObsolete Vec1;
// Assign some Values
Vec1.index[0] = 0.5;
Vec1.index[1] = 1.5;
Vec1.index[2] = 3.141;
// Now enter asm mode
__asm
{
// Some mystrery code...
movups xmm1, Vec1
mulps xmm1, xmm1
movps Vec1, xmm1
}
// End asm mode
for (int i =0;i<3;i++)
{
cout << Vec1.index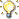
<< endl;
}
return;
}
Εάν το κάνατε σωστά θα πρέπει να πήρατε έξοδο 0.25 2.25 9.86588, τι έγινε? Πολύ απλά πήρε θα νούμερα του Vector μας και τα ύψωσε στο τετράγωνο. Πως? Με τον μαγικό κώδικα που γράψαμε σε asm, nice heh. Anyway ας γυρίσουμε πίσω στους Registers, θυμάστε στην 32bit EAX? στην ΣΕ έχουμε κάτι παρόμοιο μονο που τώρα οι Registers είναι 128bit και δεν είναι απαραίτητο να περιέχουν 1 τιμή. Τώρα τα "special" Registers είναι τα XMM0, XMM1, XMM2, XMM3, XMM4, XMM5, XMM6, XMM7 (8 στο σύνολο, και είναι ακριβώς για να μπορέσουμε να κάνουμε operations με ένα 4x4 matrix, handy ;). Όπως είπαμε και πριν κάθε μια από αυτές τις "special" Registers καταλαμβάνουν 128 bits of memory και χωράνε 4 32 bit, όπου το πρώτο καταλαμβάνει τα 0-31, το δεύτερο τα 32-63, το τρίτο τα 64-95 και το τελευταίο τα 96-127. Αυτό επίσης είναι γνώριμο πως λέγεται με τον ορισμό "Packet Single". Me to instruction Movups (Move Unaligned Packet Single) κάνουμε copy τον vector μας στην xmm1 Register (θα μπορούσαμε κάλλιστα να χρησιμοποιήσουμε και μια από τις άλλες) και χρησιμοποιούμε την movups γιατί δεν γνωρίζουμε εάν το address του διανύσματος μας Vec1, έχει γίνει aligned σε 16Byte Border στην μνήμη. Εάν γνωρίζετε ότι τα data σας έχουνε γίνει algined τότε σας προτείνω να χρησιμοποιείτε το Movaps είναι πολύ πιο γρήγορο!
Τώρα πίσω στο αρχικό μας στόχο, να φτιάξουμε ένα γρήγορο αλγόριθμο για να κάνουμε Normalize τα vectors μας! θα αρχίζω παραθέτοντας την γενική formula του normalization και μετά να την μετατρέψω σε κώδικα. Μιας και καλο θα ήταν να υπάρχει και μια non-SSE έκδοση του κώδικα σας μήπως και δεν υποστηρίζονται. Για να πετύχουμε ένα normalized Vector θα πρέπει να διατηρήσουμε την φορα και κατεύθυνση σου και να μειώσουμε το πλάτος του από 0 <= Mag <= 1, δηλαδή με απλά λόγια είναι κάτι σαν να πάρουμε το διάνυσμα μας και να το βάλουμε στην μοναδιαία σφαίρα όπου η ουρα του θα βρίσκετε το σημείο Ο(0,0) και η κορυφή του στο περίβλημα της. Η γενική formula για κάθε 3D-Vector είναι η ακόλουθη:
// Our Sample vector
v3=[x,y,z,d];
// Magnitute Calculation
|v3| = sqrt(x²+y²+z²)
// Assign Normalized Magnitute
v3_normalized = v3/|v3|
Sw κώδικα C++ θα πρέπει να ήταν ως εξής:
// Sample Vector Struct
// Where sampleVec.index[0] [ x coordinate compoment of Vector ]
// sampleVec.index[1] [ y coordinate compoment of Vector ]
// sampleVec.index[2] [ z coordinate compoment of Vector ]
// sampleVec.index[3] [ d coordinate compoment of Vector ]
// Note d is a dummy var and should be set always to 1, this is an essential step to define it
// as it's required for the matrix math to work! :O
struct sampleVec {
float index[3];
};
// Our Normalizing function
sampleVec Normalize4x1Matrix( sampleVec Vec1 )
{
// Calc Initial Magnitute
float length = sqrt( (Vec1.index[0] * Vec1.index[0]) + (Vec1.index[1] * Vec1.index[1]) + (Vec1.index[2] * Vec1.index[2]) );
// Now Normalize
for(i=0;i<3;i++)
{
Vec1.index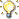 = Vec1.index 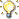/ length;
}
// Return the Product
return Vec1;
}
Στις γραμμές στις οποιες θα πρέπει να δοθεί βάση είναι αυτές που κάνουν τον υπολογισμό τις τετραγωνικής ρίζας και την διαίρεση με το υπολογισμένο magnitute. Όπως βλέπουμε στην πρώτη γραμμή έχουμε 3 προσθέσεις και 3 υπολογισμούς δυνάμεων και μια πολύ πολύ αργή sqrt() την οποια θα την εξετάσουμε με λεπτομέρεια αργότερα. Δεν θα ήταν πολύ ωραία να μπορούσαμε να κάνουμε τα 3 additions και τα 3 muls με την μια? Και όμως γίνετε, αλλα πριν προχωρήσουμε άλλο θα πρέπει να κάνουμε introduce μια άλλη τεχνική που λέγεται shuffe! Αυτή είναι η μια από τις δυσκολότερες εντολές (αν όχι η δυσκολότερη εντολή) από τις SSE για να την μάθεις, για αυτό δώστε μεγάλη προσοχή!
Το μεγαλύτερο πρόβλημα που αντιμετωπίζουμε είναι ότι με τις Registers Structure μας μπορούμε να κάνουμε operations με ίδιες συντεταγμένες δηλαδή με την Vec1.x και Vec2.x και όχι με Vec1.y και Vec2.x. και όπως δυστυχώς καταλαβαίνετε αυτό χρειαζόμαστε να κάνουμε εδώ :S! Θέλουμε να προσθέσουμε 3 συντεταγμένες του ιδιου Vector μαζί, και γεννιέται και εύλογο ερώτημα, πως θα το καταφέρουμε αυτό? Μα φυσικά με το shuffe που δεν είναι τίποτε άλλο από το να κάνει μείξεις με ανάμεσα στις Registers (καλά δεν είναι ακριβώς έτσι...αλλα για τις ανάγκες τις απλότητας το αφήνω εδώ :) ). Η πιθανή λύση αυτού του trivial "ερωτιμας" είναι να πάρουμε κάποια data από ένα block τις register και να τα κάνουμε copy σε ένα άλλο, αλλα αυτό είναι λάθος! γιατί το να μεταφέρνουμε data με τις SSE είναι πολύ αργό, εδώ θα πρέπει να αναφέρω πως το να κάνουμε copy data από την Ram στις Register είναι πολύ αργό (αργότερο και από τα General Purpose Registers) και άμα θέλουμε να πάρουμε 2 compoments θα ήτανε ακόμα πιο αργό.. blah blah...αφήστε το καλύτερα :P. Παρολαυτά υπάρχει ένας τρόπος να πάρουμε τα data που θέλουμε από τις Registers μολονότι δεν είναι και εύκολος...!
Η εντολή που κάνουμε όλη αυτή την φασαρία είναι η Shuffle (a.ka. Shuffled Packed Single). Αυτή η εντολή περιμένει 2 SSE-Registers και ένα byte Hex-String as operands. Οι πρώτες 2 θέσεις (0-63) θα διαγραφτούν και θα γραφτούν από 2 οποιαδήποτε στοιχεια του Destination Register (το πρώτο Register που δίνουμε ως operand) και οι 2 υπόλοιπες θέσεις (64-127) θα διαγραφτούν και θα γραφτούν από 2 οποιαδήποτα στοιχεια του Source Register(το δεύτερο Register που δίνουμε ως operand) Τα elements τα οποια έγιναν copy τα προσδιορίζει το 1 byte hex-string, ένα παράδειγμα είναι:
shufps xmm0, xmm1, 0x4e ; This shows the use and syntax of shuffe, xmm0 is the First Register (a.ka. Destination), xmm1 is the Second Register (a.ka. Source), and 0x4e is
; our 1 byte hex string
Φανερά φαίνεται πως θέλουμε να κάνουμε shuffle την xmm0 και αυτό σημαίνει πως όλα τα data τις xmm0 μπορεί να γίνουν overwrite ενώ η xmm1 είναι read only. Τώρα να εξηγήσουμε την χρήση της 1ής παραμέτρου (1 byte Hex-String) και για αρχή να κάνουμε decode το 4E πίσω στην διάδικοι τις μορφή... (p.s. υποθέτω πως ξέρετε πως να το "κανενε" αυτό, εάν όχι μάθετε το αλλιώς δεν θα μπορείτε να ασχοληθείτε και πολύ με τον assembler :P)
[4E]_16 = [0100 1110]_2
Νομίζω πως φαίνεται ότι μπορούμε να ξεχωρίσουμε την διάδικοι (8bit) του μορφή σε 4 ομάδες των 2bit οι οποιες είναι 01, 00, 11, 10. Μήπως σας λέει κάτι αυτό το pattern? Αυτό το Hex-String μας λέει actually τι θα γίνει copy...καλο? Παρολαυτά θα πρέπει να έχετε υπόψη πως τα PC διαβάζουν το least significant bit first για αυτό θα πρέπει να τα διαβάζετε από τα αριστερά στα δεξιά...(don't bother why, just do it ;)).
Και τώρα να τι κάνει το shuffe που γράψαμε στην προηγουμενη γραμμή!
shufps xmm0, xmm1, 0x4e:
;First element of XMM0 will be set to element 10 (the third element) of XMM0
;2nd element of XMM0 will be set to element 11 (the fourth element) of XMM0
;3rd element of XMM0 will be set to element 00 (the first element) of XMM1
;4th element of XMM0 will be set to element 01 (the second element) of XMM1
; kewl!!
Ελπίζω να σας έγινε ξεκάθαρο πια... εάν όχι... παίξτε με τον παρακάτω κώδικα.. θα σας βοηθήσει να το καταλάβετε ακόμα καλύτερα!
// Sample Vector Struct
// Where sampleVec.index[0] [ x coordinate compoment of Vector ]
// sampleVec.index[1] [ y coordinate compoment of Vector ]
// sampleVec.index[2] [ z coordinate compoment of Vector ]
// sampleVec.index[3] [ d coordinate compoment of Vector ]
// Note d is a dummy var and should be set always to 1, this is an essential step to define it
// as it's required for the matrix math to work! :O
struct sampleVec {
float index[3];
};
// Our Programs entry point
void main()
{
// Our sample vector
vectorSample Vec1;
// Let's set up some random values
Vec1.index[0] = 0.5;
Vec1.index[1] = 1.5;
Vec1.index[2] = 3.141;
Vec1.index[3] = 2; // Note we are doing here actual math...that's why I am assigning a value don't do it!! or either set it up back to 1 when you want to make multiplication
// Enter asm mode
__asm
{
// The Magic Code ;)
movups xmm0, Vec1
movaps xmm1, xmm0
mulps xmm1, xmm1
shufps xmm0, xmm1, 0x4e ; This line shuffes our registers!!
movups Vec1, xmm0
}
// Exit asm mode
// Finally output the result!
for( int i=0; i<3;i++) {
cout << Vec1.index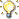 << endl;
}
// Exit
return;
}
Τι γίνετε επάνω? Πρώτα από όλα κάνουμε store το Vec1 στην xmm0 και το Vec^2 στην xmm1, μετά πραγματοποιούμε αρκιβώς το ίδιο shuffe που εξηγήσαμε παραπάνω! Εάν θέλετε δοκιμάστε να μαντέψετε τα output values χωρίς να το τρέξετε... και να είστε 100 % σίγουροι πως το κατανοήσατε πλήρως μιας και αυτό είναι πολύ σημαντικό βήμα για να καταλάβετε τα υπόλοιπα. Εάν το βρήκατε δύσκολο μην σας νoιαζει είναι από τα λίγα στοιχεια των SSE που θέλουν προσοχή... Προσπαθήστε να παίξετε λίγο με τα hex-string values να δείτε πως αλλάζουν τα shuffling των registers και μονο όταν είναι 100 % πως τα καταλάβετε να συνεχίσετε να διαβάζετε :Ο!
Applied Shuffling ftw!! Καιρός να βάλουμε όλα αυτά που δείξαμε στην πράξη!
// Sample Vector Struct
// Where sampleVec.index[0] [ x coordinate compoment of Vector ]
// sampleVec.index[1] [ y coordinate compoment of Vector ]
// sampleVec.index[2] [ z coordinate compoment of Vector ]
// sampleVec.index[3] [ d coordinate compoment of Vector ]
// Note d is a dummy var and should be set always to 1, this is an essential step to define it
// as it's required for the matrix math to work! :O
struct sampleVec {
float index[3];
};
// Our Programs entry point
void main()
{
// Our sample vector
vectorSample Vec1, Vec2;
// Let's set up some random values
Vec1.index[0] = 0.5;
Vec1.index[1] = 1.5;
Vec1.index[2] = 3.141;
Vec1.index[3] = 0; // Note we are doing here actual math...that's why I am assigning a value don't do it!! or either set it up back to 1 when you want to make multiplication
// Enter asm mode
__asm
{
// The Magic Code ;)
movups xmm0, Vec1
mulps xmm0, xmm0 ;Calculate squares
movaps xmm1, xmm0
shufps xmm0, xmm1, 0x4e ;Shuffle #1
addps xmm0, xmm1 ;Add #1
movaps xmm1, xmm0
shufps xmm1, xmm1, 0x11 ;Shuffle #2
addps xmm0, xmm1 ;Add #2
movups Vec2, xmm0
}
// Exit asm mode
// Finally output the result!
for( int i=0; i<3;i++) {
cout << Vec1.index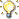 << endl;
}
// Exit
return;
}
Αυτό το κομμάτι είναι παρα πολύ γρήγορο στην εκτέλεση... αλλα έχουμε και το πρόβλημα τις sqrt() το οποίο θα πρέπει να λύσουμε... τελευταίο και καλύτερο ;). Επίσης προσέξτε ότι πρέπει το last Value του Vector μας να είναι 0 (σε αυτή την περίπτωση) για να δουλέψει το shuffle...A! και "χριεαζομαστε" 2 shuffle για να κάνουμε την δουλειά μας σωστά.. το γιατί θα σας αφήσω να το βρείτε εσείς!
Τελευταίο πρόβλημα είναι ο υπολογισμός της Sqrt() και όπως φυσικά θα γνωρίζετε εάν έχετε διαβάσει κάποιο σοβαρό βιβλίο αγλορύθμων θα έχει ένα ξεχωριστό κεφαλαιο αφιερωμένο στον γρήγορο υπολογισμό τους! Πολλοί compilers και libraries δεν έχουν πολλές version του sqrt() και exoum μια και καλή δηλαδή με διπλό accurancy (64bit). Αυτό όμως έχει μεγάλο αντίκτυπο μιας και είναι πολύ αργή και μπορείς να σώσεις μονο τα 32bit (στα 32bit systems) το οποιο φυσικά είναι πολύ ενοχλητικό...Ακόμα χειρότερα το κάνει ο "αλγοριμος" που ως επί το πλείστον χρησιμοποιείτε από τα libraries που ψάχνει την square-root κάνοντας προσεγγιστικές πράξις μέχρι να φτάσει το δοσμένο accurancy αυτό συνεπάγεται σε ένα μεγάλο αντίχτυπο στο performance! Η λύση σε όλο αυτό είναι πραγματικά απλή... θα θυσιάσουμε accurancy για perfomance (περίπου..δηλαδή). Αυτό θα ήταν έγκλημα για Scientific applications αλλα για Graphics και Multimedia Algorythms είναι ότι πρέπει! Επίσης θα πρέπει να γνωρίζουμε πως σε αυτές τις περίπτωσις χρησιμοποιούμε ένα trick το οποιο είναι οι Loop-Up Tables, που αυτό είναι να υπολογίσουμε κάποια typical values στην αρχή του προγράμματος μας όμως αυτό για να το κάνει κάποιος πρέπει να είναι πολύ καλός γνωστης μαθηματικών και έμπειρος προγραμματιστής. για καλή μας τύχη αυτό το έχει ήδη implemented το SSE για αυτό cheer!
Η εντολή στην υποία θα αναφερθούμε είναι η RSQRTPS (reciproce square root of packed single) και παίρνει 2 registers και υπολογίζει το αντίστροφο (reciprocal) τις sqrt() δηλαδή 1/sqrt() από τον "ενσωματομετο" στον CPU Loop-Up Table για κάθε element του Destination Register και του Source Register. Αυτό όμως έχει και αλλα πλεονεκτήματα μιας και μετατρέπει την διαίρεση μας σε πολλαπλασιασμό! Θα πεταχτείτε και θα πείτε τι λέει αυτός ο τρελός και που βρήκε την διαίρεση... Η διαίρεση είναι μετά τον υπολογισμό του Magnitude μας από την Sqrt() και θα πρέπει να το διαιρέσουμε με κάθε element του Vec1 μας. Επίση λοιπόν η διαίρεση είναι πολύ πιο χρονοβόρα από το τον πολλαπλασιασμό είναι σαν να έχουμε έτοιμη την formula μας! Αλλα αφού είναι Vec1 / length η Vec1 / sqrt() και μας το μετατρέπει σε Vec1 * (1/sqrt()) μιας και βρίσκει το reciprocal της sqrt() μας λύνει τα χερια! Δεν θα μπω σε details όπως τι γίνετε εάν δώσουμε αρνητικές τιμές etc... ξεφεύγει από το scope του topic! Σας αφήνω να το κοίταξε te μονοι σας! Και τώρα το τελευταίο μας polished Normalizing Program!
// Sample Vector Struct
// Where sampleVec.index[0] [ x coordinate compoment of Vector ]
// sampleVec.index[1] [ y coordinate compoment of Vector ]
// sampleVec.index[2] [ z coordinate compoment of Vector ]
// sampleVec.index[3] [ d coordinate compoment of Vector ]
// Note d is a dummy var and should be set always to 1, this is an essential step to define it
// as it's required for the matrix math to work! :O
struct sampleVec {
float index[3];
};
// Our Programs entry point
void main()
{
// Our sample vector
vectorSample Vec1;
// Let's set up some random values
Vec1.index[0] = 0.5;
Vec1.index[1] = 1.5;
Vec1.index[2] = 3.141;
Vec1.index[3] = 0; // Note we are doing here actual math...that's why I am assigning a value don't do it!! or either set it up back to 1 when you want to make multiplication
// Enter asm mode
__asm
{
// The Magic Code ;)
movups xmm0, Vec1
movaps xmm2, xmm0
mulps xmm0, xmm0
movaps xmm1, xmm0
shufps xmm0, xmm1, 0x4e
addps xmm0, xmm1
movaps xmm1, xmm0
shufps xmm1, xmm1, 0x11
addps xmm0, xmm1
rsqrtps xmm0, xmm0
mulps xmm2, xmm0
movups Vec1, xmm2
}
// Exit asm mode
// Finally output the result!
for( int i=0; i<3;i++) {
cout << Vec1.index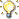 << endl;
}
// Exit
return;
}
Δεν θα βάλω comments ελπίζοντας πως μετά από όλο αυτό θα καταλαβαίνετε τι συμβαίνει.. έστω στο περίπου! Έχει πάει 5 το πρωί κουράστηκα... δεν μπορώ να γράψω άλλο... σας αφήνω... ελπίζω να μην σας κούρασε και να ήταν εύκολο στο διάβασμα... δεν ξέρω εάν βγήκε καλο έχω συνηθίσει να γράφω στα αγγλικά τέτοιου είδους stuff! tesp τώρα τα links που σας υποσχέθηκα!
Microsoft Info Regarding the Inline Assembler:
http://msdn.microsoft.com/library/en-us/vclang/html/_core_assembler_.28.inline.29_.topics.asp
Developers Info @ Intel (for SEE and Stuff)
http://www.intel.com/design/pentium4/manuals/index_new.htm
Nice article about SISD
http://arstechnica.com/articles/paedia/cpu/simd.ars
The article has Heavy References from
http://www.3dbuzz.com/vbforum/showthread.php?t=104753
Above all!! Happy Programming and wish me kali 3ekourasi!! :P
Vrika xrono mono na kanw to edit twra 8a prepi na douleboun xarma... anyway otan vrw ligo xrono akoma 8a to simplirwsw gia to optimization pou ipa, till then c ya
....